← Homepage
Implementing DFA in C
Deterministic Finite Automata (DFA) is good model for recognizing Regular Expression (RegEx). The result of a RegEx is a language. So, Simply we conclude that “DFA decides that is a specific string in a specific language or not”. From now on, I won’t get in details of DFA and RegEx any more. If you’d like to learn these, I recommend you to watch this video. Remaing part of the blogpost is about implementing a DFA in C.
Assume we have a DFA like below.
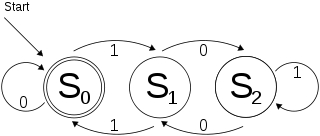
I’d like to implement a algorithm for this specific DFA. Without any reflection, anyone could choke numerous loops while designing. Besides, you will only have a algorithm for this specific DFA. It is not the smart method. I want to show you a generic and wisely method.
Firstly, Make a transaction table for this DFA. Columns represents alphabet and Rows represent states. Each elements in matrix show state number to go.
| States\Alphabet | 0 | 1 |
|---|---|---|
| S0 | S0 | S1 |
| S1 | S2 | S0 |
| S2 | S1 | S2 |
In this table, We have clear information about where to go at initial state. For example, Next alphabet symbol is 1 while DFA is in S1. So, DFA have to go S1.
Let’s assume W means input string.
#include <stdio.h>
#include <string.h> //Used for only strlen() function
int main(void){
int i; //Counter
int TransactionTable[3][2] = { //Row=state, Column=alphabet
{0, 1},
{2, 0},
{1, 2}
};
int StartingState, AcceptingState, InitialState;
StartingState = 0;
AcceptingState = 0;
InitialState = StartingState;
char w[100] = "10001011101"; //String will be processed by DFA
i = 0;
while( i < strlen(w)){ // strlen(w) means size of string
// w[i] is a char. for getting a value of a char, substracted by '0'
InitialState = TransactionTable[InitialState][(w[i] - '0')];
printf("InitialState: %d, SymbolToProcess: %d, #Transactions: %d\n", InitialState, w[i] - '0', i+1); //Only for information
i++;
}
if( InitialState == AcceptingState ){
printf("'%s' is Accepted!", w);
}
else{
printf("'%s' is Rejected.", w);
}
return 0;
}
I passed the DFA as a Transaction Table Matrix. So, I have a generic solution for DFAs. That simple! If you’d like to make a implementation for different DFA, You have to just change TransactionTable matrix, StartingState and AcceptingState variables.